Ilustración del plano complejo
¿Qué son los números complejos?
Los números complejos se introducen para dar sentido a la raíz cuadrada de los números negativos. Así se abre la puerta a un curioso al sorprendente mundo en el que todas las operaciones (salvo dividir entre 0) son posibles.
La importancia de los números complejos está marcada por sus múltiples aplicaciones en diversas Áreas (Matemáticas, Física, Ingeniería, Tecnología, ...)
Definición
Los Números Complejos son una extensión de los números reales, cumpliéndose que 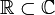 . Los números complejos tienen la capacidad de representar todas las raíces de los polinomios, cosa que con los reales no era posible.
. Los números complejos tienen la capacidad de representar todas las raíces de los polinomios, cosa que con los reales no era posible.
Esto se consigue gracias a que los complejos hacen uso de una unidad imaginaria llamada número i, que verifica la propiedad:
i2 = − 1
Esta unidad imaginaria es de hecho la que permite definir las operaciones con esos números, puesto que para efectuarlas hay que tener presente que cada lado de esa unidad imaginaria debe trabajarse en forma independiente, no confundiendo, por decirlo de alguna forma, las peras y las manzanas.
La representación binomial de un número complejo se escribe como z = a+ ib donde a es la parte real de un número complejo, y b es la parte imaginaria.
Se expresa así:
a = Re (z)
b = Im (z)
Plano de los números complejos
Desde un punto de vista geométrico la recta real (recta que representa el total de números reales) puede ser vista como un subconjunto del plano de los números complejos.
Cada número complejo sería un punto en ese plano. Usando las definiciones que siguen, se hacen posibles la suma, la resta, la multiplicación y la división entre estos puntos.
Definiremos cada complejo como un par ordenado de números reales (a, b) ó (Re(z), Im(z)), que verifican las siguientes propiedades:
(a, b) + (c, d) = (a + c, b + d)
(a, b) • (c, d) = (ac - bd, bc + ad).
Tal como los hemos definido, los números complejos forman un cuerpo, el cuerpo complejo, denotado por C (o más apropiadamente por el carácter unicode ℂ ). Si identificamos el número real a con el complejo (a, 0), el cuerpo de los números reales R aparece como un subcuerpo de C. Más aún, C forma un espacio vectorial de dimensión 2 sobre los reales. Los complejos no pueden ser ordenados como, por ejemplo, los números reales: C no puede ser convertido de ninguna manera en un cuerpo ordenado.
Aplicaciones de los números complejos
Los números complejos se usan en ingeniería electrónica y en otros campos para una descripción adecuada de las señales periódicas variables. En una expresión del tipo z = r eiφ podemos pensar en r como la amplitud y en φ como la fase de una onda sinusoidal de una frecuencia sinusoidal) como la parte real de una función de variable compleja de la forma: f(t) = z eiωt donde ω representa la frecuencia angular y el número complejo z nos da la fase y la amplitud, el tratamiento de todas las fórmulas que rigen las resistencias, capacidades e inductores pueden ser unificadas introduciendo resistencias imaginarias para las dos últimas.
Ingenieros eléctricos y físicos usan la letra j para la unidad imaginaria en vez de i que está típicamente destinada a la intensidad de corriente.
El campo complejo es igualmente importante en mecánica cuántica cuya matemática subyacente utiliza Espacios de Hilbert de dimensión infinita sobre C (ℂ).
En la relatividad especial y la relatividad general, algunas fórmulas para la métrica del espacio-tiempo son mucho más simples si tomamos el tiempo como una variable imaginaria.
En ecuaciones diferenciales, cuando se estudian las soluciones de las ecuaciones diferenciales lineales con coeficientes constantes, es habitual encontrar primero las raíces (en general complejas) del polinomio característico, lo que permite expresar la solución general del sistema en términos de funciones de base de la forma: 
Los fractales son diseños artísticos de infinita complejidad. En su versión original, se los define a través de cálculos con números complejos en el plano.



Algun ejemplo de como lo utilizamos?
ResponderEliminarEste comentario ha sido eliminado por un administrador del blog.
ResponderEliminarGracias me ayudo mucho
ResponderEliminarYo solo se que el Peluca Sabe, Putas Harry, Putas
ResponderEliminarpésima tu página visualmente hablando, malo el fondo y la letra muy chica...
ResponderEliminarTENI RAZON øTAKU QL
EliminarAún no das un ejemplo de su aplicación.
ResponderEliminarcuando minimo aumenta el tamaño de las letras, ponlas en color blanco las letras del contenido y naranja las de los titulos/subtitulos
ResponderEliminargracias
ResponderEliminarmuy buenos ejemplos
Gracias por la información.
ResponderEliminarAtiende las sugerencias, dadas en los comentarios anteriores.
Este comentario ha sido eliminado por el autor.
ResponderEliminarNos ayudo demasiado gracias 💓
ResponderEliminarMuchisimas Gracias
ResponderEliminarWnes criticones, gracias por la info <3
ResponderEliminargracias
ResponderEliminar